Options Rho: Sensitivity To Interest Rates


However, it’s still worth knowing what rho means, as it does provide another dimension of understanding as to how the price of an option may fluctuate.
What Is Rho?
Rho measures how the value of an option is sensitive to a change in risk-free interest rates. The reason this makes it the least important Greek metric is because risk-free interest rates rarely see significant or unexpected changes.
Plus, even when interest rates do fluctuate, they only have a minor impact on the price of options. This means rho has a more long-term effect (much like vega) and has only a minimal impact on short-term options.
Bear in mind, you may also see rho used for a book of several options positions. In this case, rho is in reference to the aggregated risk of exposure to changes in interest rates.
No matter if rho is being used for a single option or a book of several option positions, it is a dollar amount that represents how much the option value will change if risk-free interest rates change by a single percentage point.
Options Rho Math
It's not necessary to understand the math behind Rho (please feel free to go to the next section if you want), but for those interested rho is defined more formally as the partial derivative of options price with respect to (risk free) interest rates.
The formula for the rho of a call option is below (some knowledge of the normal distribution is required to understand it). A similar formula for a put option also exists.

Source: iotafinance
Calculating the Impact of Rho
To put the above into context, let’s say that an option has a value of $3.25, Rho is 0.5, and the risk-free interest rate is 1.5 percent. This means the price of an option will theoretically increase by $0.50 for every 1 percent increase in interest rate. Therefore, if interest rates increase by 1.5 percent to 3.5 percent, the theoretical increase will be:
$3.25 + 0.5 x 2 = $4.25
If interest rates dropped by 2 percent, we’d see a decrease instead:
$3.25 - 0.5 x 2 = $2.25
If the option has a negative rho of -0.5, the opposite will happen — the value will drop as the interest increases:
$3.25 + -0.5 x 2 = $2.25
But the value will rise when interest decreases:
$3.25 - -0.5 x 2 = $4.25
Why Do Interest Rates Affect Options?
It is easy to understand why the factors leading to sensitivity in the other Greeks impact the value of an option. For rho, it’s less obvious. After all, interest rates are for debt securities, whereas stock options are equities with no fixed interest.
To understand why interest rates affect options at all, it’s important first to be clear about what we mean by risk-free interest rates.
What Are Risk-Free Interest Rates?
In asset management, some types of investments are considered risk free. For instance, US government bonds are risk free because they’re backed by the institution of the government. As the government is unlikely to suffer severe financial troubles, there is almost no risk of savers seeing a default on their bonds.
In other words, if you purchase government bonds, you have a minimal risk of losing your investment. The risk-free interest rate is the minimum return you can receive on the money you borrow when the risk is zero.
Cost of Carry in Options
The main reason why rho matters at all is cost of carry. There’s a carrying cost of holding options because traders often borrow money to purchase financial instruments. In addition, even when a trader has money available without needing to borrow, there is a carrying cost. Traders could be investing this same amount in an account that yields interest instead. It is for these reasons that higher interest rates lead to a higher cost of carry.
As a consequence, the cost of carry is included in the price of calls — even though buying calls is cheaper than buying the underlying asset. Therefore, the cost of calls increases and decreases with the risk-free interest rate.
Rho for Calls and Puts
When rho is positive, its value increases with a higher interest rate and decreases with a lower interest rate (at least in theory). This, just like when using any of the other Greeks, assumes that all other factors remain the same.
Rho is positive for long options (long calls and short puts) but negative for short options (short calls and long puts). In other words, an increase in interest rate is generally good news for long options, whereas short options tend to benefit if interest rate decreases.
To understand why this is, let’s use an example. Imagine that ABC stock is trading at $35. To buy 100 shares would cost $3,500, but you could instead buy an at-the-money call for next month at $3.50. This means you could spend just $350 and the reward would be the same as if you bought the stock but the risk lower. Plus, if you invest the remaining $3,150 in government bonds, you’d be able to hedge your investment. If it turns out that interest rates do increase, the price of the call will also increase and become a good investment.
Furthermore, traders are more likely to buy calls when interest rates are high because of the greater savings from buying options compared to buying the underlying stock. This higher demand may also push up the price of options.
On the flip side, if interest rates are currently low, you may decide to forgo buying options and buy the underlying stock instead. This is because you’ll receive little interest keeping your money in your brokerage. Thousands of other investors will be thinking exactly the same way, meaning more people will be buying stock than call options. As a result, the price will drop for the call option.
Now let’s think about how interest impacts long puts instead. To play the underlying asset to the downside you can either short the shares or go long a put option. The first choice means you generate cash with interest. The second choice costs less, but it won’t add any more cash to your brokerage with interest. As a consequence, the first choice is more appealing when interest rates are high and it shows why high interest rates lower the value for long put options.
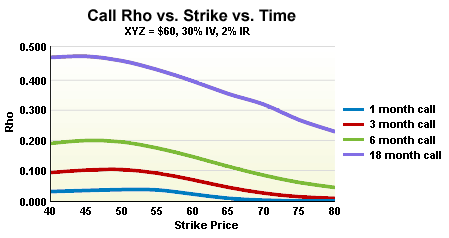
Does Volatility Impact Rho?
Volatility is a major factor for most of the Greeks, but it only has an indirect impact on the rho via the delta. How volatility affects rho will depend on whether the option is out of the money, at the money, or in the money.
Out of the Money
When options are out of the money, they have a strike price that is above (for calls) or lower than (for puts) the market price for the underlying asset. Rho has a particularly low value for options that are deep out of the money. You gain value if volatility increases, as this leads to a higher delta and subsequently a higher rho.
At the Money
Options at the money have a strike price that is close to the same (if not exactly the same) as the current market price for the underlying stock. They are little impacted by volatility. Any increase keeps the delta flat, meaning there is no change to the rho. However, looking at the rho can still be useful for at-the-money options, as it can provide an indication as to the future price trend of the underlying asset. If the option is receiving attention from investors, it is more likely to see profits.
In the Money
In-the-money call options have a strike price below market price and put options have a strike price above market price. An increase in volatility means a decrease in the delta, which translates to a decrease in the rho.
How to Use Rho
You can expect to see a higher rho for options in the money and a decrease in rho as the option moves out of the money. Rho is also higher for options that have a longer time until expiration. This is quite different from the other Greeks.
Rho will have a greater impact when interest rates change unexpectedly. This is because the sudden rate change will lead to increased market volatility in general, which causes higher option prices.
All the same, it is only really worth looking at the rho if the option has a long time until expiry — this goes for both calls and puts. This is because interest rates have a minimal impact on premium as options near expiration, due to the lower extrinsic value. For instance, rho can have an effect on long-term equity anticipation securities (LEAPs), as the expiration dates are usually at least two years.
Although rho is the least used of all the major Greek metrics, it is still worthwhile knowing what it means and how it works. Then you can decide if you want to pay attention to this metric or if you’d rather focus on the other four. If you have LEAPs, you’ll probably notice that rho does have some impact. If you trade in shorter-term options, however, you’re unlikely to notice rho making much difference.
About the Author: Chris Young has a mathematics degree and 18 years finance experience. Chris is British by background but has worked in the US and lately in Australia. His interest in options was first aroused by the ‘Trading Options’ section of the Financial Times (of London). He decided to bring this knowledge to a wider audience and founded Epsilon Options in 2012.
Related articles:



